The chain rule is used to find the partial derivatives of the feature pdf with respect to the atomic coordinates. Thus, only the derivatives of the pdf with respect to the features are listed here.
The pdf for a geometric feature ![]() (e.g., distance, angle,
dihedral angle) is
(e.g., distance, angle,
dihedral angle) is
The first derivatives with respect to feature ![]() are:
are:
| (5.40) |
The polymodal pdf for a geometric feature ![]() (e.g., distance, angle,
dihedral angle) is
(e.g., distance, angle,
dihedral angle) is
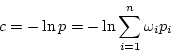 |
(5.42) |
The first derivatives with respect to feature ![]() are:
are:
When any of the normalized deviations
![]() is
large, there are numerical instabilities in calculating the derivatives
because
is
large, there are numerical instabilities in calculating the derivatives
because ![]() are arguments to the exp function. Robustness is
ensured as follows.
The `effective' normalized deviation is used in all the equations
above when the magnitude of normalized violation
are arguments to the exp function. Robustness is
ensured as follows.
The `effective' normalized deviation is used in all the equations
above when the magnitude of normalized violation ![]() is larger than
cutoff rgauss1 (10 for double precision). This scheme works up
to rgauss2 (200 for double precision); violations larger than
that are ignored. This trick is equivalent
to increasing the standard deviation
is larger than
cutoff rgauss1 (10 for double precision). This scheme works up
to rgauss2 (200 for double precision); violations larger than
that are ignored. This trick is equivalent
to increasing the standard deviation ![]() . A slight disadvantage
is that there is a discontinuity in the first derivatives at rgauss1.
However, if continuity were imposed,
the range would not be extended (this is equivalent to linearizing the
Gaussian, but since it is already linear for large deviations, a
linearization with derivatives smoothness would not introduce much
change at all).
. A slight disadvantage
is that there is a discontinuity in the first derivatives at rgauss1.
However, if continuity were imposed,
the range would not be extended (this is equivalent to linearizing the
Gaussian, but since it is already linear for large deviations, a
linearization with derivatives smoothness would not introduce much
change at all).
| (5.44) | |||
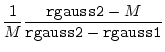 |
(5.45) | ||
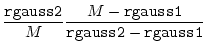 |
(5.46) | ||
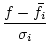 |
(5.47) | ||
| (5.48) | |||
| (5.49) |
Now, Eqs. 5.41-5.43 are used with ![]() instead
of
instead
of ![]() . For single precision,
. For single precision, ![]() , rgauss1 = 4, rgauss2 = 100.
, rgauss1 = 4, rgauss2 = 100.
The polymodal pdf for a geometric feature ![]() (e.g., a pair of
dihedral angles) is
(e.g., a pair of
dihedral angles) is
A corresponding restraint ![]() in the sum that defines the objective
function
in the sum that defines the objective
function ![]() is
is
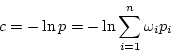 |
(5.52) |
The first derivatives with respect to features ![]() and
and ![]() are:
are:
This is like the left half of a single Gaussian restraint:
This is like the right half of a single Gaussian restraint:
This is usually used for dihedral angles ![]() :
:
| (5.58) |
The first derivatives are:
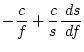 |
(5.61) | ||
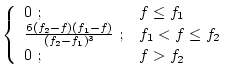 |
(5.62) |
Usually used for non-bonded distances:
The first derivatives are:
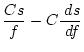 |
(5.64) | ||
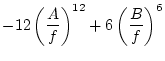 |
(5.65) |
Any restraint form can be represented by a cubic spline [Press et al., 1992]:
The first derivatives are:
| (5.71) |
The values of ![]() and
and ![]() beyond
beyond ![]() and
and ![]() are obtained by linear
interpolation from the termini. A violation of the restraint is calculated
by finding the global minimum. A relative violation is estimated by using
a standard deviation (e.g., force constant) obtained by fitting
a parabola to the global minimum.
are obtained by linear
interpolation from the termini. A violation of the restraint is calculated
by finding the global minimum. A relative violation is estimated by using
a standard deviation (e.g., force constant) obtained by fitting
a parabola to the global minimum.
Variable spacing of spline points could be used to save on memory. However, this would increase the execution time, so it is not used.
The asymmetry penalty added to the objective function is defined as
For each ![]() , the first derivatives are:
, the first derivatives are:
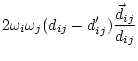 |
(5.73) | ||
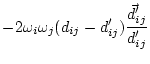 |
(5.74) |