MODELLER currently implements a Beale restart conjugate gradients algorithm [Shanno & Phua, 1980,Shanno & Phua, 1982] and a molecular dynamics procedure with the Verlet integrator [Verlet, 1967]. The conjugate gradients optimizer is usually used in combination with the variable target function method [Braun & Gõ, 1985] which is implemented with the automodel class (Section 6.4). The molecular dynamics procedure can be used in a simulated annealing protocol that is also implemented with the automodel class.
Force in MODELLER is obtained by equating the objective function ![]() with internal energy in kcal/mole. The atomic masses are all set to
that of C
with internal energy in kcal/mole. The atomic masses are all set to
that of C![]() (MODELLER unit is kg/mole). The initial velocities
at a given temperature are obtained from a Gaussian random number
generator with a mean and standard deviation of:
(MODELLER unit is kg/mole). The initial velocities
at a given temperature are obtained from a Gaussian random number
generator with a mean and standard deviation of:
| (6.7) | |||
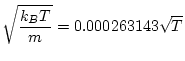 |
(6.8) |
The Newton's equations of motion are integrated by the Verlet
algorithm [Verlet, 1967]:
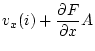 |
(6.9) | ||
| (6.10) | |||
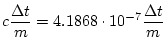 |
(6.11) |
| (6.12) | |||
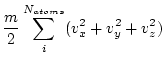 |
(6.13) |