Distance is defined by points ![]() and
and ![]() :
:
| (A.37) |
| (A.38) |
The first derivatives of ![]() with respect to Cartesian coordinates are:
with respect to Cartesian coordinates are:
| (A.39) | |||
| (A.40) |
Angle is defined by points ![]() ,
, ![]() , and
, and ![]() , and spanned by vectors
, and spanned by vectors
![]() and
and ![]() :
:
| (A.41) |
The first derivatives of ![]() with respect to Cartesian coordinates are:
with respect to Cartesian coordinates are:
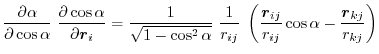 |
(A.42) | ||
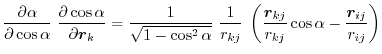 |
(A.43) | ||
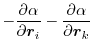 |
(A.44) |
These equations for the derivatives have a numerical instability when
the angle goes to 0 or to 180![]() .
Presently, the problem is `solved' by testing for the size
of the angle; if it is too small, the derivatives are set to 0
in the hope that other restraints will eventually pull the angle
towards well behaved regions. Thus, angle restraints of 0 or
180
.
Presently, the problem is `solved' by testing for the size
of the angle; if it is too small, the derivatives are set to 0
in the hope that other restraints will eventually pull the angle
towards well behaved regions. Thus, angle restraints of 0 or
180![]() should not be used in the conjugate gradients or molecular dynamics
optimizations.
should not be used in the conjugate gradients or molecular dynamics
optimizations.
Dihedral angle is defined by points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (
(![]() ):
):
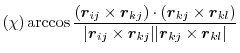 |
(A.45) |
| sign |
(A.46) |
The first derivatives of ![]() with respect to Cartesian coordinates are:
with respect to Cartesian coordinates are:
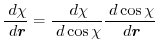 |
(A.47) |
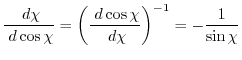 |
(A.48) |
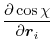 |
(A.49) | ||
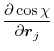 |
(A.50) | ||
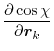 |
(A.51) | ||
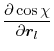 |
(A.52) | ||
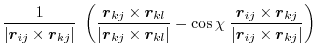 |
(A.53) | ||
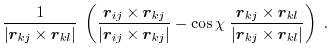 |
(A.54) |
These equations for the derivatives have a numerical instability when the angle goes to 0. Thus, the following set of equations is used instead [van Schaik et al., 1993]:
| (A.55) | |||
| (A.56) | |||
| (A.57) | |||
| (A.58) | |||
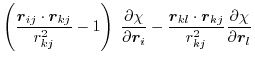 |
(A.59) | ||
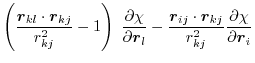 |
(A.60) |
The only possible instability in these equations is when the length of
the central bond of the dihedral, ![]() , goes to 0. In such a case,
which should not happen, the derivatives are set to 0. The expressions for
an improper dihedral angle, as opposed to a dihedral or dihedral angle,
are the same, except that indices
, goes to 0. In such a case,
which should not happen, the derivatives are set to 0. The expressions for
an improper dihedral angle, as opposed to a dihedral or dihedral angle,
are the same, except that indices ![]() are permuted to
are permuted to ![]() .
In both cases, covalent bonds
.
In both cases, covalent bonds ![]() ,
, ![]() , and
, and ![]() are defining
the angle.
are defining
the angle.
This is the accessibility value calculated by the PSA algorithm (see model.write_data()). This is usually set by the last call to Restraints.make() or Restraints.make_distance(). First derivatives are not calculated, and are always returned as 0.
Atomic density for a given atom is simply calculated as the number of atoms within a distance energy_data.contact_shell of that atom. First derivatives are not calculated, and are always returned as 0.
The absolute atomic coordinates ![]() ,
, ![]() and
and ![]() are available
for every point
are available
for every point ![]() , primarily for use in anchoring points to planes, lines
or points. Their first derivatives with respect to Cartesian coordinates
are of course simply 0 or 1.
, primarily for use in anchoring points to planes, lines
or points. Their first derivatives with respect to Cartesian coordinates
are of course simply 0 or 1.